Motivation
Bereits 1954 stellten Dantzig, Fulkerson & Johnson eine Methode zur Lösung des TSP vor, die auf linearer Programmierung beruht — die sogenannten cutting planes. Mit dieser Methode lösten sie eine 49-Städte-Instanz, eine beeindruckende Leistung zur damaligen Zeit. Auch der aktuelle Weltrekord, eine optimale Tour durch 15.112 Städte in Deutschland, wurde von Applegate, Bisby, Chvátal & Cook mit einer Weiterentwicklung der cutting planes-Methode gelöst.
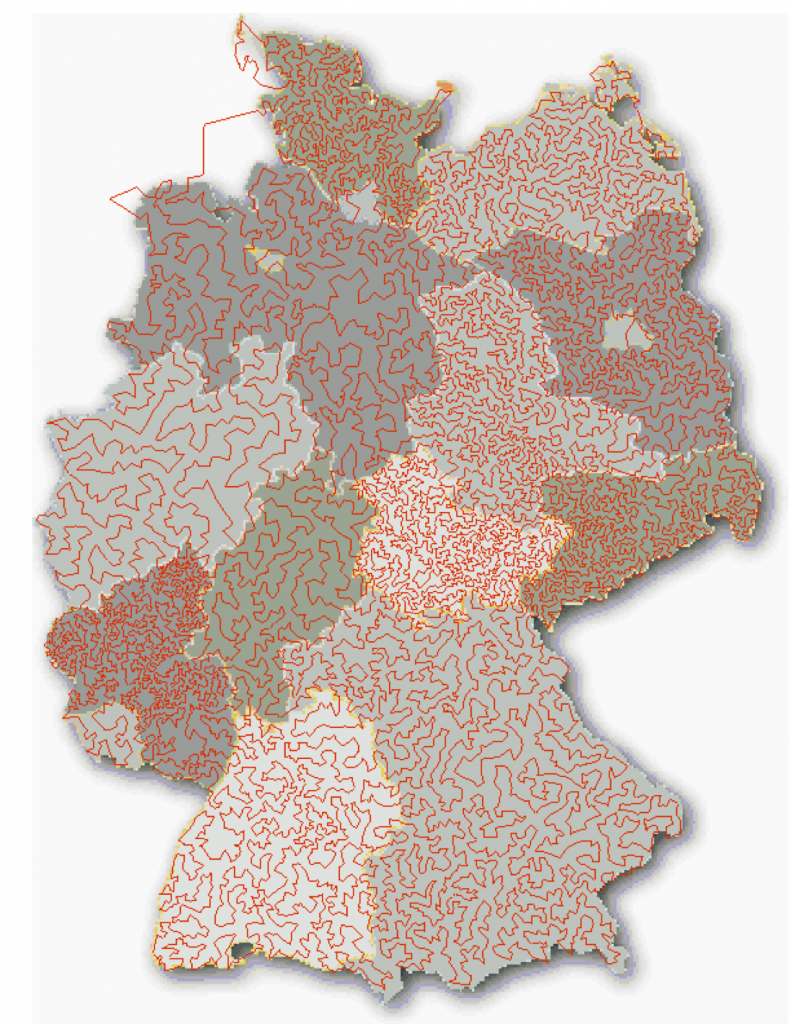
Abb. 1: Lösung des traveling salesman problems für 15.112 Städte in Deutschland (Quelle)
Einführung und Beispiele der vorliegenden Ausarbeitung orientieren sich vor allem an [CLR:01], die Lösungsansätze zur Behandlung des traveling salesman problems mithilfe der linearen Programmierung an [Applegate:98] und [Applegate:01]. Diese Arbeit gibt erst eine kurze Einführung in dielineare Programmierung; diese wird sowohl formal als auch anschaulich erläutert. Anschließend wird vorgestellt, wie das TSP mithilfe der cutting planes-Methode gelöst werden kann, die auf der linearen Programmierung basiert.
Lineare Programmierung (LP)
Grundidee der linearen Programmierung ist die Optimierung einer linearen Funktion mit ![]() Freiheitsgraden, die durch lineare Gleichungen und Ungleichungen eingeschränkt ist. Diese Einschränkungen können z.B. widersprüchliche Bedingungen oder beschränkte Ressourcen darstellen.
Freiheitsgraden, die durch lineare Gleichungen und Ungleichungen eingeschränkt ist. Diese Einschränkungen können z.B. widersprüchliche Bedingungen oder beschränkte Ressourcen darstellen.
Die lineare Programmierung ist eines der Hauptverfahren des Operations Research,[1]Operations Research ist ein Teilgebiet der angewandten Mathematik, das sich mit dem Optimieren bestimmter Prozesse oder Verfahren beschäftigt. Die beiden Hauptgebiete sind lineare und nicht-lineare Optimierung. um lineare Optimierungsprobleme zu lösen. Dabei stellt sie eine sehr allgemeine Methode zur Optimierung von Problemlösungen dar, für die keine speziell entwickelten Algorithmen bekannt sind.
Einführendes Beispiel
Angenommen ein Politiker möchte seine Wahlkampfgelder möglichst effizient einsetzen, d.h. einerseits so wenig wie möglich ausgeben, aber andererseits in der Stadt mit 100.000 Einwohnern, der Vorstadt mit 200.000 Einwohnern und auf dem Land mit 50.000 Einwohnern jeweils eine absolute Mehrheit erringen.
Abhängig davon, in welches Wahlkampfthema er investiert, steigt oder sinkt seine Beliebtheit in den drei Bevölkerungsgruppen, was sich direkt auf seinen Wahlerfolg auswirkt:
| Wahlkampfthema | Variable | Stadt | Vorstadt | Land |
|---|---|---|---|---|
| Straßenbau | 5 | 3 | ||
| Waffenkontrolle | 8 | 2 | ||
| Subventionen | 0 | 0 | 10 | |
| Mineralölsteuer | 10 | 0 |
Die Tabelle ist folgendermaßen zu interpretieren: Werden 1000 EUR in den Wahlkampf für Straßenbau investiert, sinken die erwarteten Wählerstimmen in der Stadt um 2000, nehmen in Vorstadt aber um 5000 und auf dem Land um 3000 zu. Analog für die restlichen drei Zeilen.
Die erwarteten Gewinne bzw. Verluste in der Stadt lassen sich, wenn die vier Variablen ![]() belegt sind, zusammenfassen als
belegt sind, zusammenfassen als ![]() . Um die Bedingung der absoluten Mehrheit zu erfüllen, unterliegt dieser Wert der (linearen) Einschränkung
. Um die Bedingung der absoluten Mehrheit zu erfüllen, unterliegt dieser Wert der (linearen) Einschränkung ![]() . Ähnliches gilt wieder für die beiden anderen Bevölkerungsgruppen, so dass sich das gesamte Problem formal zusammenfassen lässt:
. Ähnliches gilt wieder für die beiden anderen Bevölkerungsgruppen, so dass sich das gesamte Problem formal zusammenfassen lässt:
![]()
unter Einhaltung der Nebenbedingungen für eine Mindestanzahl an Wählerstimmen:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcrcrcrcr} -2 x_1 &+& 8 x_2 &+& 0 x_3 &+& 10 x_4 &\geq& 50 \\ 5 x_1 &+& 2 x_2 &+& 0 x_3 &+& 0 x_4 &\geq& 100 \\ 3 x_1 &-& 5 x_2 &+& 10 x_3 &-& 2 x_4 &\geq& 25 \end{array} \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-ec4cada847279452bd6aa1df7f840735_l3.png)
![]()
Das Problem der linearen Programmierung ist es nun, diese Aufgabe zu lösen. Zwar ist es bei einfacheren Problemen wie diesem nicht weiter schwierig, durch Ausprobieren eine gültige Lösung zu finden. Aber bereits bei der Suche nach der optimalen Lösung kommt man damit nicht mehr weiter. Dafür gibt es effiziente Verfahren, die in Kapitel Methoden zur Lösung von LP-Problemen vorgestellt werden.
Weitere Anwendungsbeispiele
Viele Probleme, die sich mit linearer Programmierung lösen lassen, sind im wirtschaftlichen Bereich zu finden. Ein Beispiel dafür ist die effiziente Verteilung von Crews einer Airline auf alle möglichen Flüge unter Einhaltung gesetzlicher Bestimmungen, z.B. der maximalen Arbeitszeit oder der Verteilung auf Flugzeugtypen. Weitere Anwendungsbeispiele finden sich in vielen Operation Research-Büchern.
Aber nicht nur wirtschaftliche Optimierungsaufgaben lassen sich mit linearer Programmierung lösen, sondern auch abstraktere Probleme, beispielsweise in der Graphentheorie: das Finden kürzester Pfade, des maximalen Flusses oder eines minimalen Kostenflusses lässt sich unter geeigneter Formulierung ebenfalls lösen. Näheres hierzu findet sich auch in [CLR:01].
Formale Formulierung
Ziel der linearen Programmierung ist es, eine lineare Funktion in Abhängigkeit von einer Menge linearer Ungleichungen zu optimieren. Sei ![]() und
und ![]() eine Menge von Variablen. Dann nennt man
eine Menge von Variablen. Dann nennt man ![]() mit
mit
![Rendered by QuickLaTeX.com \[ f(x_1, \dots, x_n) = c_1 x_1 + c_2 x_2 + \dots + c_n x_n = \sum_{i=1}^n c_i x_i \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-2c363c1c26742696eb01bb30d489ae24_l3.png)
eine lineare Funktion. Sei ![]() und
und ![]() eine lineare Funktion. Dann ist
eine lineare Funktion. Dann ist
![]()
eine lineare Gleichung und
![]()
sind lineare Ungleichungen. In der linearen Programmierung sind strikte Ungleichungen nicht zugelassen. Formal ist ein LP-Problem das Problem, eine lineare Funktion in Abhängigkeit von einer endlichen Anzahl linearer Ungleichungen zu optimieren. Man bezeichnet das Problem als lineares Minimierungsproblem oder lineares Maximierungsproblem.
Wie wir im Abschnitt Normalformen zeigen, sind alle linearen Programme äquivalent zu einem LP-Problem in Standardform. Dies ist dann folgendermaßen definiert:
![Rendered by QuickLaTeX.com \[ \text{maximiere } f(x_1, \dots, x_n) = \sum_{i=1}^n c_i x_i \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-58c5f3ad7838d923db21fd292104069a_l3.png)
unter Einhaltung der linearen Bedingungen
![Rendered by QuickLaTeX.com \[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.defined.de/wp-content/ql-cache/quicklatex.com-6e985acdd864f1450741da5f405e4139_l3.png" height="82" width="350" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} \sum_{j=1}^n a_{ij} x_j &\leq b_i & \text{für } i = 1,2,\dots,m \\ x_j &\geq 0 & \text{für } j = 1,2,\dots,n \end{align*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-eb1ec3db8d8643f710307ffba29745c3_l3.png)
Dasselbe Problem lässt sich in Matrix-Schreibweise definieren als
![]()
unter den Nebenbedingungen[2]Zu diesem Zweck ist es nötig, die Relationen ![]() und
und ![]() geeignet auf Vektoren zu definieren: Seien
geeignet auf Vektoren zu definieren: Seien ![]() . Dann gilt
. Dann gilt ![]() gdw.
gdw. ![]() .
. ![]() analog.
analog.
![]()
Da dieses Problem bereits in einer standardisierten Form vorliegt, kann man es kompakt als ![]() zusammenfassen. Für die vorkommenden Matrizen und Vektoren gelten die Dimensionen
zusammenfassen. Für die vorkommenden Matrizen und Vektoren gelten die Dimensionen ![]() und
und ![]() .
.
Normalformen
Unter einer Normalform eines mathematischen Objekts versteht man in der Mathematik eine Darstellung, die bestimmte vorgegebene Eigenschaften hat und für alle Objekte dieses Typs eindeutig bestimmt werden kann.
Im Bereich der linearen Programmierung gibt es zwei Normalformen, die von Interesse sind: In der Standardform sind alle Bedingungen durch Ungleichungen definiert, in der Slackform durch Gleichungen. Jedes LP-Problem lässt sich durch geeignete Umformungen in beide Normalformen bringen. Mögliche Abweichungen von der Standardform sind
- Minimierungsproblem statt Maximierungsproblem,
- Variablen ohne Nichtnegativitätsbedingung,
- Gleichheitsbedingungen statt Ungleichheitsbedingungen und
- Größer-als-Bedingungen statt Kleiner-als-Bedingungen.
Formulierungen von linearen Optimierungsproblemen, in denen diese Fälle auftreten, lassen sich umformen durch einige einfachen Operationen:
- Negierung des Koeffizienten
 in der Zielfunktion,
in der Zielfunktion, - Ersetzung von
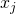 durch
durch 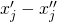 mit
mit 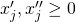 ,
, - Ersetzung von
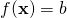 durch
durch 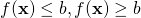 und
und - Negierung der Koeffizienten
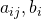 in der betreffenden Bedingung
in der betreffenden Bedingung 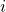 .
.
Beispiel
Gegeben sei das folgende lineare Optimierungsproblem:
![]()
unter Einhaltung der Nebenbedingungen:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcrcr} x_1 & + & x_2 & = & 7 \\ x_1 & - & 2 x_2 & \leq & 4 \\ x_1 & & & \geq & 0 \end{array} \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-9f0e88db9295fa4c402f23233b7d5340_l3.png)
Durch schrittweise Anwendung der obigen Regeln lässt sich dieses lineare Programm in Standardform überführen. Man erhält dann das äquivalente Optimierungsproblem:
![]()
unter folgenden Nebenbedingungen:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcrcrcr} x_1 & + & x_2 & - & x_3 & \leq & 7 \\ -x_1 & - & x_2 & + & x_3 & \leq & -7 \\ x_1 & - & 2 x_2 & + & 2 x_3 & \leq & 4 \\ \end{array} \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-47be14336223581b4837d78887da29f8_l3.png)
![]()
Um ein LP-Problem in Standardform in die Slackform zu überführen, verwendet man die Äquivalenz der folgenden beiden Ausdrücke:
![Rendered by QuickLaTeX.com \[ \sum_{j=1}^n a_{ij} x_j \leq b_i \qquad \Longleftrightarrow \qquad 0 \leq s_i = b_i - \sum_{j=1}^n a_{ij} x_j \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-082dd8e07742487be840183ad6a10f43_l3.png)
Die ![]() nennt man Slack-Variablen. Außer den Nichtnegativitätsbedingungen erhält man nur noch Gleichungen als Nebenbedingungen. Die Slackform eines LP-Problems ist besonders für die praktische Anwendung des Simplex-Algorithmus von Bedeutung, die hier nicht näher erläutert wird.
nennt man Slack-Variablen. Außer den Nichtnegativitätsbedingungen erhält man nur noch Gleichungen als Nebenbedingungen. Die Slackform eines LP-Problems ist besonders für die praktische Anwendung des Simplex-Algorithmus von Bedeutung, die hier nicht näher erläutert wird.
Geometrische Interpretation
Es gibt eine sehr intuitive geometrische Interpretation von linearen Optimierungsproblemen, die das allgemeine Verständnis verbessern kann. Diese bezieht sich in der folgenden Erläuterung auf lineare Programme in Standardform; aber für äquivalente Darstellungen lässt sich eine analoge Interpretation
finden.
Geht man von einer linearen Gleichung über die Variablen ![]() aus, so beschreibt diese eine Hyperebene im
aus, so beschreibt diese eine Hyperebene im ![]() -dimensionalen Raum, d.h. alle Punkte
-dimensionalen Raum, d.h. alle Punkte ![]() , die die entsprechende Gleichung erfüllen, liegen in dieser Hyperebene.[3]Eine Hyperebene im
, die die entsprechende Gleichung erfüllen, liegen in dieser Hyperebene.[3]Eine Hyperebene im ![]() -dimensionalen Raum ist eine
-dimensionalen Raum ist eine ![]() -dimensionale, lineare Manigfaltigkeit, die den Raum in zwei Hälften spaltet. Im 2-dimensionalen ist das z.B. eine Gerade, im 3-dimensionalen eine Ebene. Die zugehörige lineare Ungleichung beschreibt dann einen Halbraum, nämlich alle Punkte, die auf der einen Seite der Hyperebene liegen (inkl. der Hyperebene selbst). Dieser Halbraum stellt die Menge aller gültigen Lösungen für die gegebene Ungleichung dar. Hierbei erklärt sich auch, warum keine strikten Ungleichungen zugelassen sind: Lösungen eines linearen Optimierungsproblems sind Punkte auf den durch die Ungleichungen definierten Trenngeraden. Bei strikten Ungleichungen könnte man die Punkte, die dann neben der Trenngeraden liegen, nicht bestimmen.
-dimensionale, lineare Manigfaltigkeit, die den Raum in zwei Hälften spaltet. Im 2-dimensionalen ist das z.B. eine Gerade, im 3-dimensionalen eine Ebene. Die zugehörige lineare Ungleichung beschreibt dann einen Halbraum, nämlich alle Punkte, die auf der einen Seite der Hyperebene liegen (inkl. der Hyperebene selbst). Dieser Halbraum stellt die Menge aller gültigen Lösungen für die gegebene Ungleichung dar. Hierbei erklärt sich auch, warum keine strikten Ungleichungen zugelassen sind: Lösungen eines linearen Optimierungsproblems sind Punkte auf den durch die Ungleichungen definierten Trenngeraden. Bei strikten Ungleichungen könnte man die Punkte, die dann neben der Trenngeraden liegen, nicht bestimmen.
Kombiniert man mehrere lineare Ungleichungen zu einem Ungleichungssystem, so erhält man als Lösungsmenge gerade die Punkte, die alle Ungleichungen erfüllen, also den Schnitt der Halbräume. Dieser Schnitt erzeugt immer ein konvexes Polytop[4]Ein konvexes Polytop lässt sich definieren als die konvexe Hülle über eine endliche Menge von Punkten. Ein Polytop kann man sich außerdem vorstellen als die Verallgemeinerung von Polygon und Polyeder auf höhere Dimensionen. (bzw. einen Simplex, nach dem der Simplex-Algorithmus in Abschnitt Simplex-Algorithmus benannt ist).[5]Ein geometrischer Körper ![]() ist konvex, wenn für alle Punktepaare
ist konvex, wenn für alle Punktepaare ![]() mit
mit ![]() die Verbindungsstrecke zwischen
die Verbindungsstrecke zwischen ![]() und
und ![]() komplett in
komplett in ![]() liegt.
liegt.
Die zu maximierende Zielfunktion stellt ebenfalls eine Hyperebene dar, allerdings mit noch unbekanntem Abstand vom Ursprung und damit unbekanntem Zielwert. Lässt man eine Ebene mit der entsprechenden Steigung vom unendlichen auf den Ursprung zuwandern, so ist die Lösung erreicht, sobald die Ebene zum ersten Mal den Simplex berührt.
Beispiel
Gegeben sei das folgende lineare Optimierungsproblem:
![]()
unter Einhaltung folgender Nebenbedingungen:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcrcr} 4 x_1 &-& x_2 &\leq& 8 \\ 2 x_1 &+& x_2 &\leq& 10 \\ 5 x_1 &-& 2 x_2 &\leq& - 2 \\ &x_1,x_2& &\geq& 0 \end{array} \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-59ce5f14b48dcc39ddaf6e512e7bc00a_l3.png)
In Abbildung 2 ist die geometrische Veranschaulichung dieses Beispiels zu sehen. Die Lösung des Problems ist die obere Ecke des Polygons, die von der Geraden geschnitten wird.
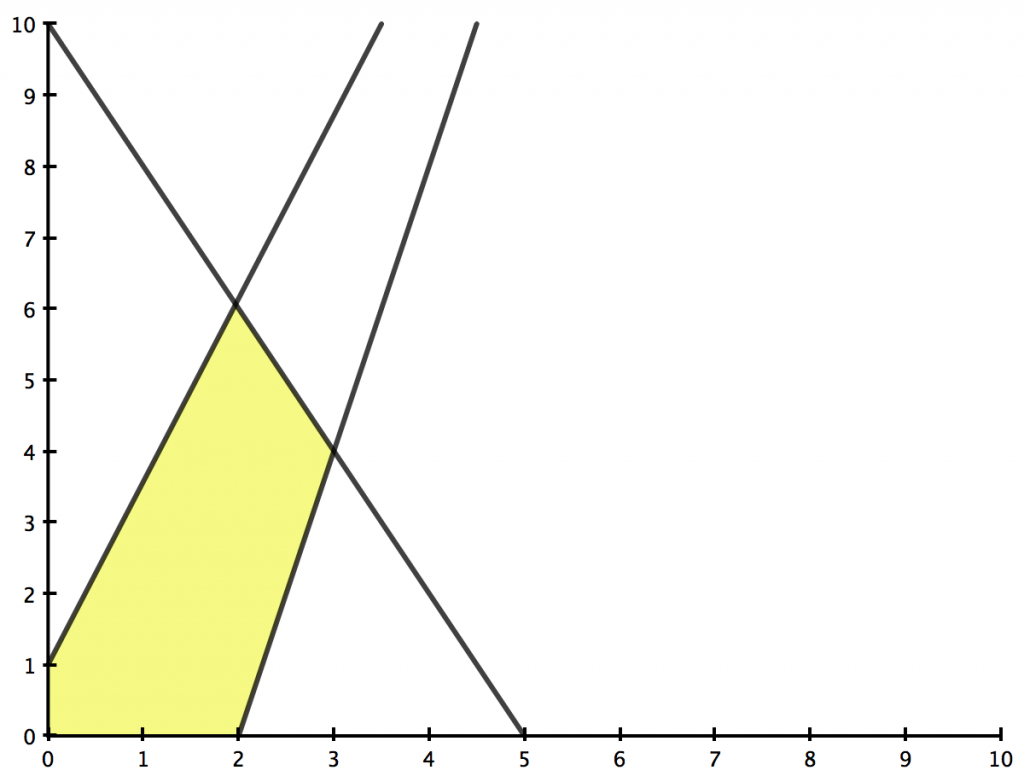
Abb. 2(a): Geometrische Interpretation eines linearen Programms. Konvexer Schnitt dreier Halbräume, die durch entsprechende lineare Ungleichungen definiert sind.
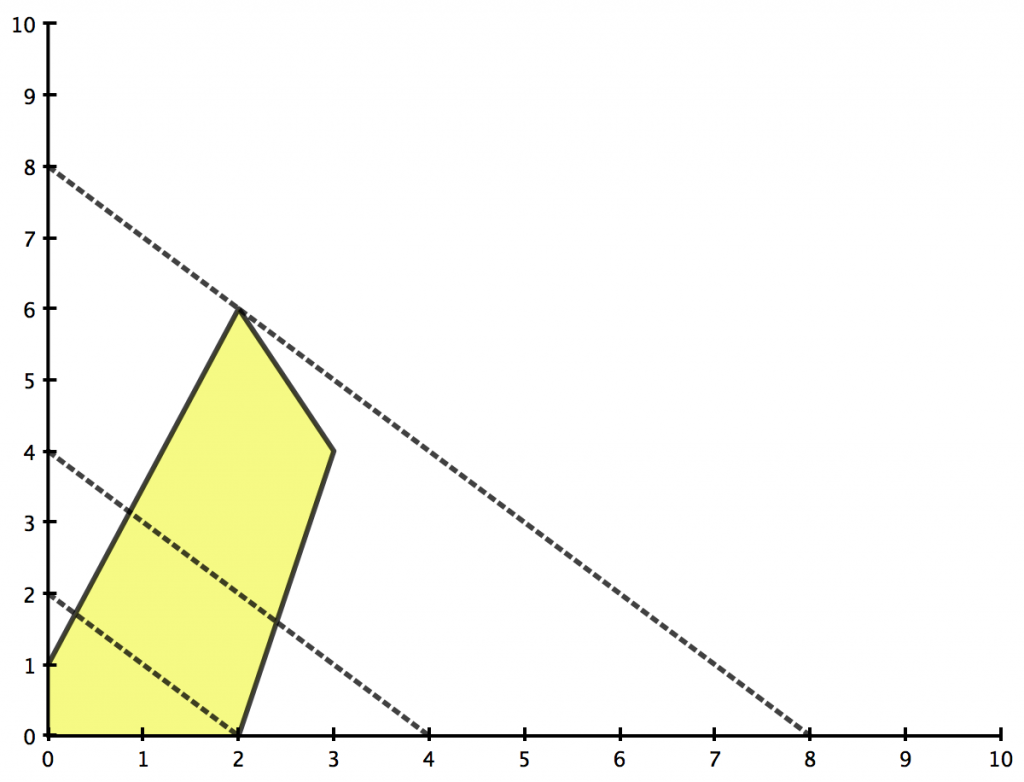
Abb. 2(b): Geometrische Interpretation eines linearen Programms. Mögliche Schnitte mit einer Zielfunktion
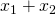 (nach [CLR:01]).
(nach [CLR:01]).Spezialfall: diskrete lineare Programmierung
Ein Spezialfall der linearen Programmierung ist die sogenannte diskrete lineare Programmierung (engl. integer linear programming). Bei diesen Optimierungsproblemen muss zusätzlich zu den Einschränkungsungleichungen noch gelten ![]() , d.h. für die Variablen
, d.h. für die Variablen ![]() werden nur ganzzahlige Werte zugelassen.
werden nur ganzzahlige Werte zugelassen.
Durch diese zusätzliche Bedingung wird der Raum der Lösungen natürlich weiter eingeschränkt. In Abb. 3 ist das beispielhaft in zwei Dimensionen zu sehen. Dennoch sind die Extremwerte des Polytops noch immer reellwertig. Daher liefern die bekannten Algorithmen für lineare Programme in diesem Fall keine gültige Lösung. Man versucht z.B., dieses Problem zu umgehen, indem man schrittweise das Ungleichungssystem erweitert, bis die durch ein Standard-Verfahren ermittelte, reellwertige Lösung eine ganze Zahl ist. Dieses Verfahren wird in Abschnitt Schnittebenen beschrieben.
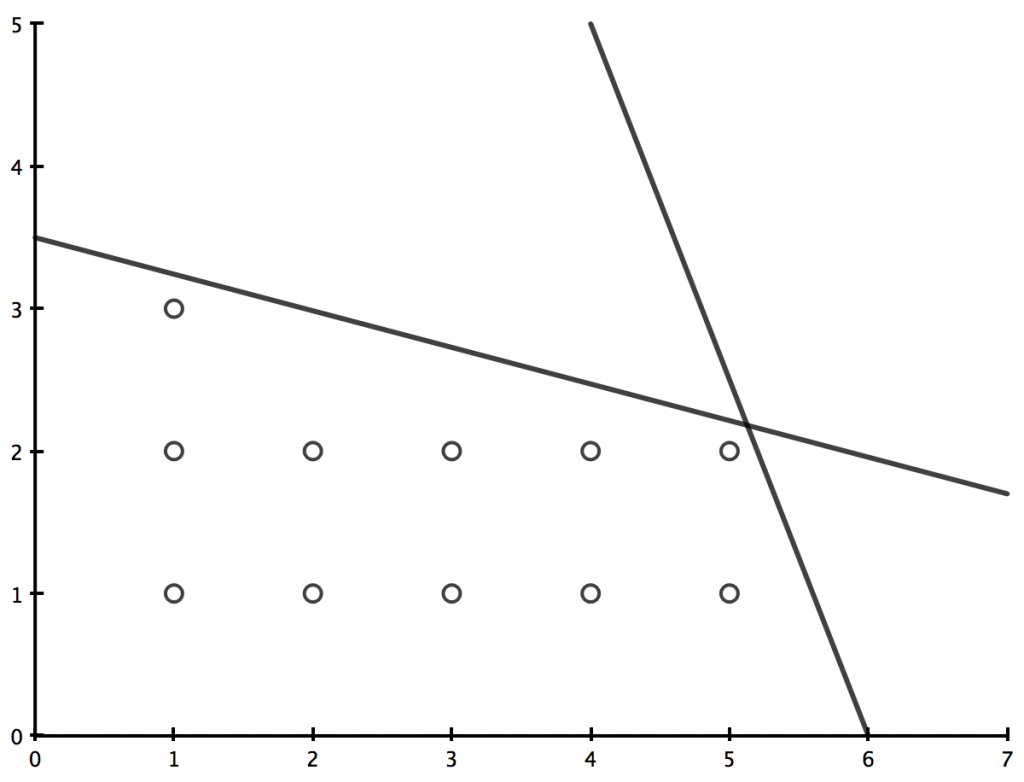
Abb. 3: Lösungsraum eines diskreten linearen Optimierungsproblems sind in diesem Beispiel nur die markierten Punkte. Ein effizientes Finden eines solchen Punktes ist nicht möglich.
Eine weitere Spezialisierung dieser Art von Problemen ist die binäre diskrete lineare Programmierung (engl. 0-1 integer linear programming), bei der gelten muss ![]() , also die
, also die ![]() nur die beiden Werte 0 oder 1 annehmen.
nur die beiden Werte 0 oder 1 annehmen.
Auch das traveling salesman problem lässt sich als (binäres) diskretes lineares Programm darstellen, wie wir in Abschnitt Lösung des TSP mithilfe von LP sehen werden. Leider ist diese Art von Problemen nicht effizient lösbar, da sie in die Klasse der ![]() -harten Probleme fällt. Dies scheint anschaulich nicht klar, lässt sich aber leicht durch polynomielle Reduktion auf ein
-harten Probleme fällt. Dies scheint anschaulich nicht klar, lässt sich aber leicht durch polynomielle Reduktion auf ein ![]() -vollständiges Problem beweisen, beispielsweise 3SAT oder KNAPSACK.
-vollständiges Problem beweisen, beispielsweise 3SAT oder KNAPSACK.
Methoden zur Lösung von LP-Problemen
Es existieren bereits einige fertige Standardverfahren zur Lösung von linearen Optimierungsproblemen, die in einer Normalform vorliegen. Daher müssen solche Probleme nicht mit einer speziellen Lösung angegangen werden, sondern es genügt, ein entsprechendes lineares Programm zu formulieren und einen passenden Algorithmus darauf auszuführen.
Lange Zeit dachte man, dass die lineare Programmierung nicht der Problemklasse ![]() angehört, bis der russische Mathematiker L. G. Khachian 1979 einen effizienten Algorithmus zur Lösung solcher Probleme vorstellte — das sogenannte Ellipsoidverfahren. Dies liegt allerdings in der Effizienzklasse
angehört, bis der russische Mathematiker L. G. Khachian 1979 einen effizienten Algorithmus zur Lösung solcher Probleme vorstellte — das sogenannte Ellipsoidverfahren. Dies liegt allerdings in der Effizienzklasse ![]() und ist daher für den praktischen Einsatz nicht geeignet.
und ist daher für den praktischen Einsatz nicht geeignet.
Einen völlig neuen Ansatz stellte N. K. Karmarkar vor: die interior point-Methode mit einer Effizienz von ![]() , die es von der Geschwindigkeit her mit dem im folgenden beschriebenen Simplex-Algorithmus aufnehmen kann.
, die es von der Geschwindigkeit her mit dem im folgenden beschriebenen Simplex-Algorithmus aufnehmen kann.
Simplex-Algorithmus
Der Simplex-Algorithmus ist die in der Praxis am häufigsten eingesetzte Methode zur Lösung von linearen Optimierungsproblemen. Zwar lassen sich Anwendungsfälle konstruieren, in denen dieses Verfahren keine polynomielle Laufzeit mehr aufweist, doch in der Praxis löst es die Mehrzahl aller Aufgaben effizient. Der ursprüngliche Algorithmus wurde 1947 von Dantzig vorgestellt und im Laufe der Zeit deutlich verbessert.
Wie aus dem Namen abzulesen ist, nutzt der Simplex-Algorithmus die Simplex-Form des Lösungsraums aus, um seine Aufgabe zu bearbeiten. Der Algorithmus erhält als Eingabe ein lineares Programm in Slackform und berechnet dann eine optimale Lösung.
Anschaulich beginnt das Verfahren an einer Ecke des Polytops und führt eine Kette von Iterationen durch, bei denen der Algorithmus jeweils zu einer benachbarten Ecke springt, sofern deren Wert nicht kleiner als der aktuelle ist. Der Wert berechnet sich natürlich durch Einsetzen der Ecke als Lösung in
die Zielfunktion.
Der Algorithmus terminiert, sobald er ein lokales Maximum findet, d.h. keine benachbarte Ecke einen höheren Zielwert aufweist. Dieses Maximum ist global wegen der Konvexität des Polytops und der Linearität der Zielfunktion. Der ausführliche Beweis findet sich in [CLR:01].
Lösung des TSP mithilfe von LP
Lösungsansatz
Um das symmetrische traveling salesman problem mit den hier vorgestellten Methoden zu lösen, beschreiben wir es auf formale Weise in einer Art, die bereits an die lineare Programmierung erinnert: Gegeben sei ein TSP mit ![]() Städten, spezifiziert durch einen Kostenvektor
Städten, spezifiziert durch einen Kostenvektor ![]() , also einem Vektor mit einer Komponente für jede mögliche Verbindung zweier Städte. Jede mögliche Tour sei durch einen Inzidenzvektor
, also einem Vektor mit einer Komponente für jede mögliche Verbindung zweier Städte. Jede mögliche Tour sei durch einen Inzidenzvektor ![]() dargestellt, wobei
dargestellt, wobei ![]() die Menge der Touren darstellt (alle Hamilton-Zyklen). Der Inzidenzvektor gibt dabei an, ob die zu einer Komponente
die Menge der Touren darstellt (alle Hamilton-Zyklen). Der Inzidenzvektor gibt dabei an, ob die zu einer Komponente ![]() gehörige Kante in der Tour enthalten ist (
gehörige Kante in der Tour enthalten ist (![]() ) oder nicht (
) oder nicht (![]() ).
).
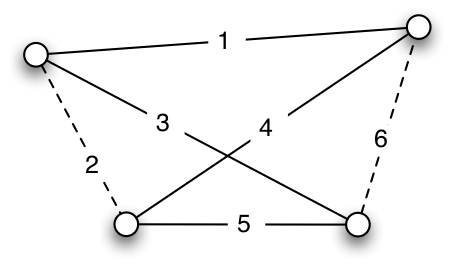
Abb. 4: Alle Verbindungen zwischen vier Städten und eine der gültigen Touren. Der Inzidenzvektor lautet in diesem Fall
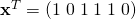 und beschreibt, welche Kanten in der Lösung enthalten sein sollen.
und beschreibt, welche Kanten in der Lösung enthalten sein sollen.Da ![]() genau die Kosten einer Tour
genau die Kosten einer Tour ![]() ergibt, lautet das traveling salesman problem dann:
ergibt, lautet das traveling salesman problem dann:
![Rendered by QuickLaTeX.com \[ <a name="id1144194015"></a><span class="ql-right-eqno"> (1) </span><span class="ql-left-eqno"> </span><img src="https://www.defined.de/wp-content/ql-cache/quicklatex.com-1c844bbe7f44c6fca75c41660d141786_l3.png" height="18" width="196" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \text{minimiere } \mathbf{c}^T\mathbf{x} \text{ mit } \mathbf{x} \in \mathcal{S} \end{equation*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-f4c5b1be58e1ea09b057bdad0c9c7720_l3.png)
Allerdings hat man nun ein Problem, das so nicht ohne weiteres lösbar ist. Daher formuliert man eine relaxation, d.h. ein erweitertes Problem, das allerdings einfacher zu behandeln ist:
![Rendered by QuickLaTeX.com \[ <a name="id1695410238"></a><span class="ql-right-eqno"> (2) </span><span class="ql-left-eqno"> </span><img src="https://www.defined.de/wp-content/ql-cache/quicklatex.com-1ae57d32ffef533728f23e17938802e0_l3.png" height="21" width="214" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \text{minimiere } \mathbf{c}^T\mathbf{x} \text{ mit } A\mathbf{x} \leq \mathbf{b}, \end{equation*}" title="Rendered by QuickLaTeX.com"/> \]](https://www.defined.de/wp-content/ql-cache/quicklatex.com-a7c64674c88156767806fd9f68c938f7_l3.png)
wobei ![]() ein lineares Ungleichungssystem ist, das von allen
ein lineares Ungleichungssystem ist, das von allen ![]() erfüllt wird. Das bedeutet, jede gültige Lösung von (1) ist auch eine Lösung für (2), aber nicht umgekehrt. Man erhält ein lineares Problem
erfüllt wird. Das bedeutet, jede gültige Lösung von (1) ist auch eine Lösung für (2), aber nicht umgekehrt. Man erhält ein lineares Problem ![]() , das mit den Standardmethoden wie dem Simplex-Algorithmus gelöst werden kann.
, das mit den Standardmethoden wie dem Simplex-Algorithmus gelöst werden kann.
Natürlich ist die Lösung von (2) nicht direkt geeignet für das ursprüngliche Problem: Einerseits hat der Lösungsraum evtl. eine größere Ausdehnung, da gefordert ist, dass er mindestens alle gültigen Touren mit einschließt. Andererseits wurde die Bedingung der diskreten Variablenbelegungen fallengelassen, um ein effizientes Verfahren anwenden zu können. Diese Bedingung muss natürlich im Laufe der Berechnung wieder aufgenommen werden, z.B. indem man nach der Ausgabe einer Lösung prüft, ob sie wirklich aus diskreten Werten besteht.
Auf zwei Arten kann man die Lösung aber dennoch ausnutzen: man findet zumindest eine untere Schranke für das gegebene traveling salesman problem. Eine untere Schranke kann man beispielsweise dazu nutzen, den ermittelten Wert eines Näherungsverfahrens qualitativ einzuschätzen — liegt er nahe an der Schranke, genügt er vielleicht schon und man muss nicht weitersuchen. Außerdem kann man mit einer Lösung von (2) in der Nähe davon nach einer Lösung für (1) suchen.
Initiales LP-Problem
Zuerst ist es nötig, ein initales LP-Problem aufzustellen, das die Bedingungen der relaxation erfüllt. Da der Inzidenzvektor ![]() nur die Werte 0 und 1 annehmen kann, soll gelten:
nur die Werte 0 und 1 annehmen kann, soll gelten:
![]()
Zu beachten ist, dass so auch nicht-diskrete Werte zugelassen werden, d.h. eine bestimmte Kante ist zu einem Bruchteil zwischen 0 und 1 in einer Tour enthalten, was anschaulich natürlich keinen Sinn macht.
Als weitere einschränkende Bedingung berücksichtigt man, dass jede Stadt ![]() auf einer Rundreise nur von genau zwei Kanten besucht wird:
auf einer Rundreise nur von genau zwei Kanten besucht wird:
![]()
Diese Bedingungen werden von allen ![]() erfüllt und können daher als initiales LP-Problem verwendet werden. Um jetzt zu einer Lösung für das eigentliche Problem
erfüllt und können daher als initiales LP-Problem verwendet werden. Um jetzt zu einer Lösung für das eigentliche Problem ![]() zu kommen, muss man den Lösungsraum Schritt für Schritt einschränken. Dies geschieht mit Hilfe von cutting planes, die im nächsten Abschnitt beschrieben werden.
zu kommen, muss man den Lösungsraum Schritt für Schritt einschränken. Dies geschieht mit Hilfe von cutting planes, die im nächsten Abschnitt beschrieben werden.
Schnittebenen
Hat das erweiterte Problem ![]() eine Lösung und das Polytop
eine Lösung und das Polytop ![]() einen Extrempunkt, dann findet ein LP-Algorithmus (z.B. der Simplex-Algorithmus) diesen Randpunkt als optimale Lösung
einen Extrempunkt, dann findet ein LP-Algorithmus (z.B. der Simplex-Algorithmus) diesen Randpunkt als optimale Lösung ![]() . Jetzt gilt es zwei Fälle zu betrachten: Ist
. Jetzt gilt es zwei Fälle zu betrachten: Ist ![]() , so hat man die optimale Lösung für das zugehörige TSP gefunden. Andernfalls existiert wegen der Konvexität des Lösungsraums eine lineare Ungleichung, die von allen Punkten in
, so hat man die optimale Lösung für das zugehörige TSP gefunden. Andernfalls existiert wegen der Konvexität des Lösungsraums eine lineare Ungleichung, die von allen Punkten in ![]() erfüllt wird, aber von
erfüllt wird, aber von ![]() nicht. Man nennt diese Ungleichung Schnittebene (engl. cutting plane oder cut) und fügt sie zum Ungleichungssystem
nicht. Man nennt diese Ungleichung Schnittebene (engl. cutting plane oder cut) und fügt sie zum Ungleichungssystem ![]() hinzu. Dieser Schritt wird wiederholt bis zur Entdeckung einer gültigen Lösung.
hinzu. Dieser Schritt wird wiederholt bis zur Entdeckung einer gültigen Lösung.
Die größte Schwierigkeit hierbei ist das automatische Finden der Schnittebenen bis zur optimalen Lösung für das TSP. Hierfür existieren verschiedene Methoden. 1958 stellte Gomory die nach ihm benannten Gomory cuts vor, die aber aus Effizienzgründen heute nicht mehr verwendet werden. Stattdessen werden vor allen Dingen Hypergraph-Schnitte[6]Ein Hypergraph ist die Verallgemeinerung eines Graphen mit Kanten über beliebig viele Knoten. verwendet. Beispiele dafür sind subtour inequalities, blossom inequalities und comb inequalities, die in [Aapplegate:98] und [Applegate:01] detaillierter vorgestellt werden.
Subtour inequalities
Dies sind die intuitivsten Ungleichungen, die automatisch zu bestimmen sind. Ihnen zugrunde liegt die Tatsache, dass eine gültige Tour jede Aufteilung der Städte ![]() in zwei echte Teilmengen
in zwei echte Teilmengen ![]() und
und ![]() die beiden Teilmengen durch mindestens zwei Kanten verbinden muss. Dies lässt sich leicht einsehen, da der Handlungsreisende beim Wechsel von einer Stadt aus
die beiden Teilmengen durch mindestens zwei Kanten verbinden muss. Dies lässt sich leicht einsehen, da der Handlungsreisende beim Wechsel von einer Stadt aus ![]() in eine Stadt aus
in eine Stadt aus ![]() wieder in eine der Städte aus
wieder in eine der Städte aus ![]() zurückkehren muss, um seine Tour zu vollenden. Veranschaulicht ist dies in Abbildung 5.
zurückkehren muss, um seine Tour zu vollenden. Veranschaulicht ist dies in Abbildung 5.
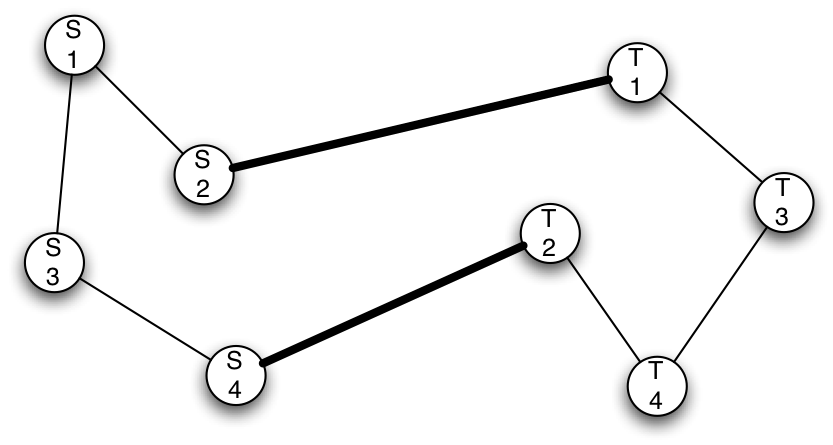
Abb. 5: Die Menge der Städte wurde hier aufgeteilt in zwei echte Teilmengen S und T. Fett markiert sind die beiden Verbindungskanten zwischen diesen Teilmengen. Jede gültige Tour enthält mindestens zwei solcher Verbindungskanten.
Die Zahl der Verbindungskanten zwischen den Knotenmengen ![]() und
und ![]() ist definiert als
ist definiert als
![]()
denn gezählt wird jede vorhandene Kante, die sowohl Knoten aus ![]() als auch Knoten aus
als auch Knoten aus ![]() enthält. Die subtour-Bedingung lässt sich dann formal angeben als
enthält. Die subtour-Bedingung lässt sich dann formal angeben als ![]() . Man erhält also eine Ungleichung, mit der das Polytop von einigen nicht-gültigen Lösungen bereinigt wird.
. Man erhält also eine Ungleichung, mit der das Polytop von einigen nicht-gültigen Lösungen bereinigt wird.
In einem iterativen Verfahren wird das anfängliche Ungleichungssystem jeweils um eine deratige Ungleichung erweitert, falls eine subtour in der gefundenen Lösung des erweiterten Problems auftritt. Es gibt effiziente Methoden, in der erneuten Berechnung einer Lösung mit einem erweiterten Ungleichungssystem die Ergebnisse vorheriger Berechnung einzubeziehen.
Zusammenfassung
Lineare Programmierung ist eines der Standardverfahren zur exakten Lösung größerer Instanzen des traveling salesman problem. Man kann diese Aufgabe als Problem der binären diskreten linearen Programmierung auffassen. Diese Gruppe von Problemen ist ![]() -hart und daher nicht effizient lösbar. Zur Lösung kommt man, indem man effiziente Verfahren der einfachen linearen Programmierung iterativ anwendet, während man ein hochdimensionales Polytop, das den Lösungsraum darstellt, mit geeigneten cut-Bedingungen immer weiter beschneidet.
-hart und daher nicht effizient lösbar. Zur Lösung kommt man, indem man effiziente Verfahren der einfachen linearen Programmierung iterativ anwendet, während man ein hochdimensionales Polytop, das den Lösungsraum darstellt, mit geeigneten cut-Bedingungen immer weiter beschneidet.
Aufgrund der schwierigen Lösbarkeit dieser Aufgabe, bietet sich das hier beschriebene Verfahren vor allem dann an, wenn unbedingt die exakte Lösung berechnet werden muss. Für Fälle, in denen eine Näherungslösung ausreicht, existieren verschiedene heuristische Verfahren, die bedeutend schneller zum Erfolg führen.
Literatur
[Applegate:98] David Applegate, Robert Bixby, Vašek Chvátal, and William Cook. On the solution of traveling salesman problems. Documenta Mathematica, Extra Volume Proceedings ICM III (1998):645–656, 1998.
[Applegate:01] David Applegate, Robert Bixby, Vašek Chvátal, and William Cook. TSP cuts which do not conform to the template paradigm. Lecture Notes in Computer Science, 2241:261–305, 2001.
[CLR:01] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to algorithms, chapter Linear Programming, pages 770–821. The MIT Press, Cambridge, Massachusetts, second edition, 2001.
[GP:99] Martin Grötschel and Manfred W. Padberg. Die optimierte Odyssee. Spektrum der Wissenschaft, Digest, 2:32–41, 1999.
References
| ↑1 | Operations Research ist ein Teilgebiet der angewandten Mathematik, das sich mit dem Optimieren bestimmter Prozesse oder Verfahren beschäftigt. Die beiden Hauptgebiete sind lineare und nicht-lineare Optimierung. |
|---|---|
| ↑2 | Zu diesem Zweck ist es nötig, die Relationen |
| ↑3 | Eine Hyperebene im |
| ↑4 | Ein konvexes Polytop lässt sich definieren als die konvexe Hülle über eine endliche Menge von Punkten. Ein Polytop kann man sich außerdem vorstellen als die Verallgemeinerung von Polygon und Polyeder auf höhere Dimensionen. |
| ↑5 | Ein geometrischer Körper |
| ↑6 | Ein Hypergraph ist die Verallgemeinerung eines Graphen mit Kanten über beliebig viele Knoten. |